DIMENSI TIGA - Jarak Titik ke Titik

 

Tujuan Pembahasan

Setelah pembahasan materi ini, diharapkan kalian dapat mendeskripsikan jarak antar titik dalam ruang. Selain itu, dapat menjelaskan prosedur menentukan jarak titik ke titik, dan menentukan jarak titik ke titik dalam ruang bidang datar.

Dalam kehidupan sehari-hari, banyak kita temukan penerapan dari konsep jarak dalam ruang. Coba perhatikan gambar berikut.

Gambar 1. Cable Stayed Bridge (Jembatan Kabel Penahan/kabel tetap)

Gambar di atas adalah gambar Jembatan Barelang yang menghubungkan antara Pulau Batam, Pulau Tonton, Pulau Nipah, Pulau Rempang, Pulau Galang dan Pulau Galang Baru. Dalam perencanaan pembangunannya tentunya diperlukan perhitungan panjang kabel penahan yang pada dasarnya merupakan jarak antar titik dalam ruang berdimensi tiga.

Contoh lain penerapan konsep jarak dalam ruang yang sangat dekat dengan kita adalah pembuatan kuda-kuda suatu rumah seperti gambar berikut.

Gambar 2. Kuda-kuda suatu rumah

Tentunya kalian sering melihat bentuk kuda-kuda rumah seperti gambar di atas. Untuk menghemat biaya pembuatan rumah, salah satu aspek yang harus diperhatikan adalah biaya pembuatan kuda-kuda rumah. Penentuan Rincian Anggaran (RAB) pembuatan kuda-kuda dapat ditentukan dengan matematika. Untuk mendapatkan rincian biaya tersebut, salah satu konsep yang dapat digunakan adalah dimensi tiga. Konsep yang dimaksud jarak titik dengan titik atau titik dengan garis.

Nah, bagaimana cara menghitung panjang kabel yang diperlukan seperti pada pembuatan Jembatan Barelang atau panjang kayu yang diperlukan untuk membuat kuda-kuda untuk atap rumah? Untuk itu kita akan membahas pada modul ini materi jarak dalam ruang bidang datar yang terdiri atas jarak antara titik, jarak titik ke garis, dan jarak titik ke bidang.

Konsep jarak titik ke titik

Sebelum mengetahui pengertian dari jarak tiitik ke titik, kalian harus mengetahui konsepnya terlebih dahulu. yuk kita perhatikan telebih dahulu dua contoh masalah di bawah ini untuk mengetahui bagaimana konsep dari jarak titik ke titik.

Contoh 1

Gambar kota dan Jalan yang menghubungkannya

Gambar di atas menunjukkan kota-kota yang terhubung dengan jalan. Sebuah titik mempresentasikan kota dan ruas garis mempresentasikan jalan yang menghubungkannya.

Mari kita umpamakan kalian sedang berada di kota A dan berencana ingin berangkat menuju kota C. Selanjutnya kalian tentukan kemungkinan rute-rute yang akan kalian pilih dan tentukan penjang rute-rute tersebut. Manakah rute yang terpendek? Kemudian berapakah jarak antara kota A ke kota C? Setelah dapat, berikan alasannya.

Nah, untuk menyelesaikan masalah di atas. Pertama-tama buat sebuah tabel kemungkinan rute yang akan kalian pilih seperti berikut.

Dari tabel di atas kalian akan melihat bahwa rute terpendek dari kota A ke kota C adalah rute yang pertama. Rute tersebut yakni  A → C sepanjang 30 km.

Jadi, jarak antara kota A ke kota C adalah 30 km yang merupakan jarak lintasan terendek yang menghubungkan kota tersebut.

Contoh 2

Jarak dua titik pada lingkarang

Dua buah lingkarang di atas memiliki masing-masing titik dan ruas garis yang menghubungkannya. Titik A, B, C, D, dan E terletak pada lingkaran L1 dan titik P, Q, R, S, dan T terletak pada lingkaran L2. Tentukan ruas garis manakah yang mewakili jarak antara kedua lingkarang tersebut?

Untuk menjawab pertanyaan contoh permasalahan di atas, perlu kalian ketahui bahwa dalam geometri jarak antara dua bangunan yakni ruas garis terpendek yang menghubungkan dua titik pada kedua bangunan tersebut. Dalam gambar tersebut sudah terlihat jelas bahwa ruas garis terpendek dari pada yang lainnya yakni ruas garis CR. Maka dari itu ruas garis CR merupakan jarak antara lingkaran L1 dan lingkaran L2.

Nah, dari kedua contoh permasalahan di atas kalian pasti sudah bisa menyimpulkan pengertian dari jarak titik ke titik kan?

Pengertian jarak titik ke titik

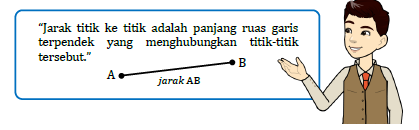
Jadi, jarak titik ke titik adalah panjang ruas garis terpendek yang menghubungkan titik-titik tersebut. Dalam geometri pun, jarak dua bangun didefinisikan sebagai panjang ruas garis terpendek yang menghubungkan dua titik pada bangun-bangun tersebut.

Latihan Soal

Nah, setelah mengetahui konsep dan pengertian dari jarak titik ke titik dalam ruang bidang datar saatnya kita latihan soal. Simak baik-baik ya contoh soal berikut ini.

Diketahui kubus ABCD.EFGH dengan panjang rusuk 20 cm.

 Hitunglah jarak antara titik-titik berikut.

a. B ke F
b. A ke D
c. G ke H
d. A ke C
e. H ke B
f. G ke titik tengah AB

Jawab:

a. Jarak titik B ke F merupakan salah satu rusuk dari kubus ABCD.EFGH. Karena kubus memiliki panjang rusuk yang sama, jadi jarak titik B ke F adalah 20 cm.

b. Jarak titik A ke D merupakan salah satu rusuk dari kubus ABCD.EFGH. Karena kubus memiliki panjang rusuk yang sama, jadi jarak titik A ke D adalah 20 cm.

c. Jarak titik G ke H merupakan salah satu rusuk dari kubus ABCD.EFGH. Karena kubus memiliki panjang rusuk yang sama, jadi jarak titik G ke H adalah 20 cm.

d. Jarak titik A ke C diwakili oleh panjang ruas garis AC. Ruas garis AC merupakan diagonal bidang alas ABCD.

Dari gambar di atas, bisa kita perhatikan ABC adalah segitiga siku-siku di B. Oleh karena itu, untuk menghitungnya kita bisa menggunakan Teorema Pythagoras sebagai berikut:

Jadi, jarak titik A ke C adalah 20√2 cm.

e. Jarak titik H ke B diwakili oleh panjang ruas garis HB. Ruas garis HB merupakan diagonal ruang kubus ABCD.EFGH.

Dari gambar di atas, bisa kita perhatikan bahwa segitiga BDH adalah segitiga siku-siku di D. Ruas garis BD adalah diagonal bidang alas ABCD, sehingga BD = AC = 20√2 cm (hasil perhitungan pada bagian d).

Bisa kita perhatikan juga BDH adalah segitiga siku-siku di D. Oleh karena itu, untuk menghitungnya kita bisa menggunakan Teorema Pythagoras sebagai berikut:

Jadi, jarak titik H ke B adalah 20√3 cm.

f. Misalkan P adalah titik tengah AB. Jarak titik G ke titik tengah AB diwakili oleh panjang ruas garis GP seperti ditunjukkan pada gambar berikut.

Dari gambar di atas, bisa kita perhatikan bahwa segitiga BGP adalah segitiga siku-siku di B. Ruas garis BG adalah diagonal bidang alas BCGF, sehingga BG = 20√2 cm (panjang BG = AC = BD, semuanya adalah diagonal bidang kubus ABCD.EFGH).

Bisa kita perhatikan juga BGP adalah segitiga siku-siku di B. Oleh karena itu, untuk menghitungnya kita bisa menggunakan Teorema Pythagoras sebagai berikut:

Jadi, jarak titik G ke P titik tengah AB adalah 30 cm.

Nah, itu lah seputar materi jarak titik ke titik dalam ruang bidang datar. Jadi, intinya jarak titik ke titik adalah panjang ruas garis terpendek yang menghubungkan titik-titik tersebut. Semoga Bermanfaat yaa!!

Sumber:

Modul Matematika Umum Kelas XII KD 3.1
@2020, Direktorat SMA, Direktorat Jenderal PAUD, DIKDAS dan DIKMEN 7

Read More